Een wiskundige kleurenkubus maken

Deze kubus is eigenlijk een bundeling van niet minder dan 6 wiskundige thema’s, één per zijvlak: We bespreken de kleuractiviteiten per zijvlak:

1. Vierkleurenstelling
2. Tessellatie
3. Cellulaire automata
4. Ulams spiraal
5. Latijns vierkant
6. Concentrische cirkels

1. Vierkleurenstelling De vierkleurenstelling stelt dat iedere tweedimensionele kaart kan ingekleurd worden met slechts vier verschillende kleuren, zonder dat ooit twee aangrenzende stukken op de kaart in dezelfde kleur zullen zijn.

Deze stelling is beroemd in de geschiedenis van de wiskunde. Ze werd 1852 door Francis Guthrie als vermoeden gesteld, en hoewel de formulering simpel lijkt, ging een eeuw met onvolledige bewijzen voorbij voordat de stelling kon bewezen worden, In 1976 lukte het Kenneth Appel en Wolfgang Haken om de stelling te bewijzen, maar met de hulp van een computer die de vele mogelijke gevallen van aangrenzing moest controleren. Omdat het bewijs te lang was en delen ervan enkel met de computer geverifieerd waren, was er enig ophef rond de vierkleurenstelling. Enerzijds was het één van de eerste belangrijkere stellingen die met de hulp van de computer werd bewezen, een praktijk die ondertussen bij de wiskundigen meer ingeburgerd is. Anderzijds vonden filosofen het problematisch dat een bewijs te lang kon worden om nog door een mens gelezen te worden, een discussie die tot op de dag van vandaag aanhoudt. Ondertussen werd de stelling ook via een andere weg, maar nog steeds met behulp van een computer bewezen, en werd het bewijs ook via automatische (computer)verificatie gecontroleerd.

2. Tessellatie Tessellatie is eigenlijk niets meer dan een tegeling of vlakvulling. Je hebt één (of meerdere) element(en), waarmee je een gegeven oppervlak moet tegelen. Voor de hand liggende tegelingen kunnen gemaakt worden met de klassieke tegelvormen: vierkant, rechthoek, ruit, of ook een regelmatig zeshoek. Maar ook meer onregelmatige vormen laten toe om een gegeven oppervlakte te betegelen. Hoewel tegelen van oudsher in vele culturen wordt gedaan, is het pas in de 20e eeuw dat ook wiskundigen zich voor tegelen beginnen te interesseren. Naast de vraag of je met gegeven vormen een gegeven oppervlak kan betegelen, is er ook de vraag welke patronen gegeven tegelvormen kunnen maken, herhalen ze zich of herhalen ze zich niet? Zo is bijvoorbeeld de Penrose-tegeling een tegeling met twee vormen die geen repetitief patroon oplevert.

3. Cellulaire automata Cellulaire automata werden in de jaren 1940-1950 uitgevonden in het kader van het bedenken van formele modellen die rekenen konden formaliseren. Stanislas Ulam en John von Neumann waren bij de eerste om dergelijke modellen te onderzoeken. Het idee is simpel: je hebt een tweedimensioneel veld met “cellen” (praktisch gezien een papier gevuld met vierkanten, zoals in een wiskundeschriftje). Je kleurt een aantal cellen van de eerste rij zwart en je kiest een aantal regels hoe de tweede rij cellen, alnaargelang de cellen van de eerste rij, in te kleuren zijn. Iedere cel van de tweede rij heeft drie “voor”- cellen, één linksachter, één direct achter en één rechtsachter. Alnaargelang hoe deze drie cellen gekleurd zijn krijgt de cel zijn kleur. In totoal heb je dus 8 regels (2x2x2) nodig, voor de acht mogelijke kleuringen van de 3 voorgangerscellen, zoals in volgend voorbeeld:

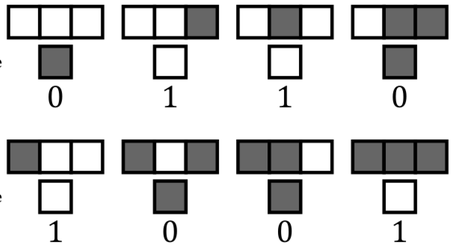
In de jaren 1980-1990 heeft Stephen Wolfram, bekend van zijn wiskundige software Mathematica, een systematische studie van alle cellulaire automata gemaakt. Door middel van computerberekeningen classifieerde Wolfram alle 256 binaire automaten in vier klasses:

1. automata die naar een stabiele toestand evolueren
2. automata die naar een herhalende of oscillerende structuur gaan
3. automata die naar een scjinbaar chaotische of willekeurige toestand gaan
4. automata waarbinnen complexere interactie tussen structuren en willekeur optreedt.

4. Ulams Spiraal In 1963 vond Stanislaw Ulam een grafische voorstelling van de priemgetallen, die een jaar later door Martin Gardner in zijn Scientific American column werd gepopulariseerd. Ulams

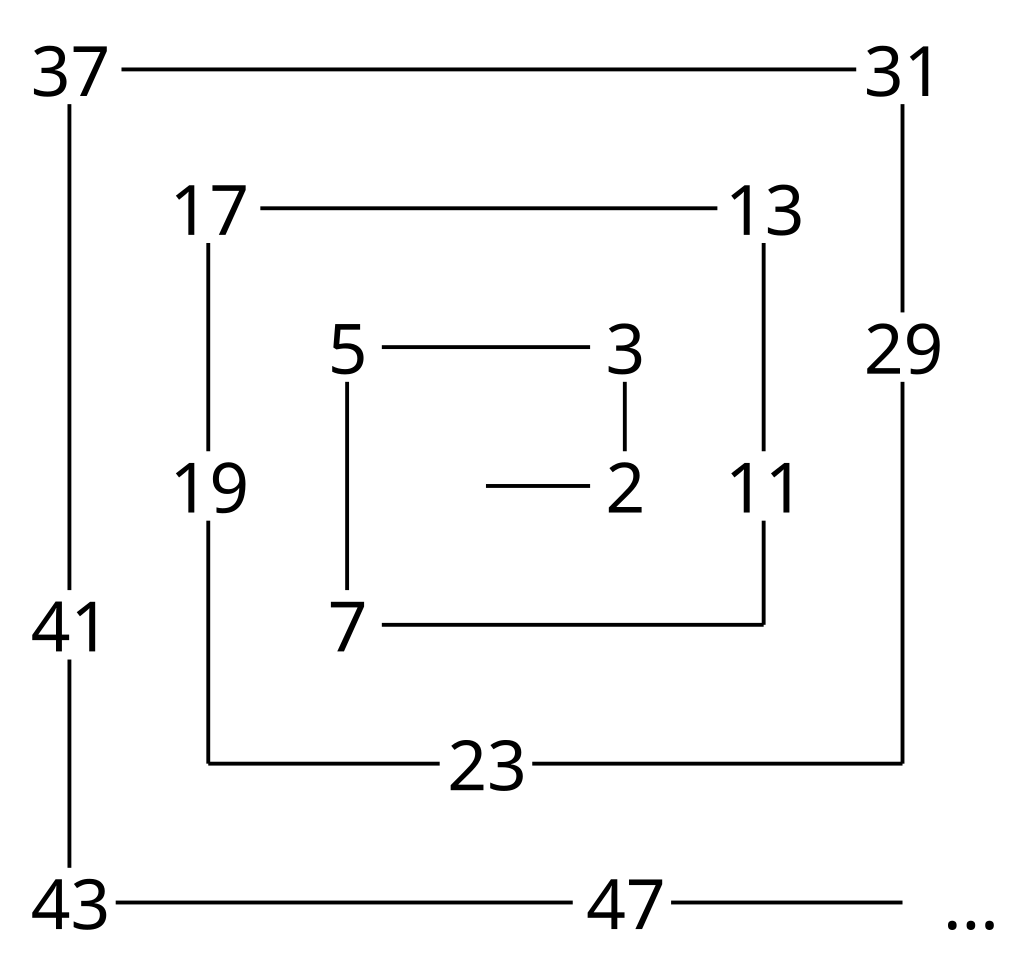
idee was om de gehele getallen niet per rij op een blad te schrijven,maar in spiraalvorm. In het midden van je (vierkante) blad schrijf je de 1 en dan spiraalsgewijs in tegenwijzerzin vervolg je met de andere gehele getallen 2, 3, enzovoort, zoals hieronder aangegeven: Als je nu de priemgetallen binnen de gehele getallen aanduidt, dan krijg je een merkwaardig patroon, de priemgetallen lijken allemaal op diagonalen te liggen:

5. Latijns vierkant Een Latijns vierkant is een vierkant van n rijen en n kolommen, waarbij in elke rij en in elke kolom n verschillende tekens staan (met slecht n verschillende tekens ter beschikking). Als deze symbolen getallen zijn, dan is bijgevolg de som van elke rij en elke kolom dezelfde, deze vierkanten noemt men magische vierkanten of tovervierkanten. Deze magische vierkanten duiken als sinds de oudheid op, zowel in de Griekse, Romeinse als in de Arabische cultuur. Uit die tijd komen ook de oudste wiskundige behandelingen, die methodes geven hoe je efficient een magisch vierkant kunt vullen. De eerste uitputtende wiskundige behandelingen die niet alleen methodes geven maar ook toelaten alle mogelijke magische vierkanten te construeren, dateren uit de 18de eeuw, in het bijzonder ook in een studie van de hand van de grote wiskundige Leonhard Euler (1707- 1783).

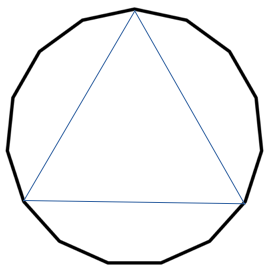
6. Concentrische cirkels Als je in een cirkel een regelmatige veelhoek tekent, en van hoekpunt naar hoekpunt springt en de hoekpunten telkens met een draad verbindt, maak je kleinere veelhoeken binnenin de oorspronkelijke regelmatige veelhoek, of ook een omgeschreven cirkel binnenin de oorspronkelijke cirkel, als je tenminste altijd sprongetjes van dezelfde afstand maakt. Als de lengte van je sprongetjes (m) geen gemeenschappelijke deler heeft met het aantal hoekpunten van je veelhoek (n), dan is die kleinere veelhoek opnieuw een regelmatige veelhoek met n hoekpunten.. Als de lengte van je sprongetjes wel een gemeenschappelijke deler (d) heeft met het aantal hoekpunten van de veelhoek, dan krijg je een kleine veelhoek die niet n hoekpunten heeft, maar wel n/d hoekpunten. 1 Bijvoorbeeld, bij een regelmatige vijftienhoek, de hoekpunten genummerd van 1 tot 15 in wijzerzin, kun je springen per 7 op volgende wijze: 1, 8, 15, 22=15+7=7, 14, 21=15+6=6, 13, 19=15+4=4, 11, 18=15+3=3, 10, 17=15+2=2, 9, 16=15+1=1 en zo ben je in vijftien stappen terug rond.

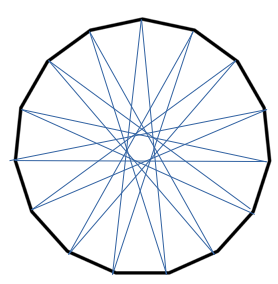
Kies je daarentegen voor sprongetjes per 5 dan heb je een gemeenschappelijke deler met 15 (5 namelijk). Dan spring je korter als volgt: 1, 6, 11, 16=15+1=1 en je bent rond en jet hebt een regelmatige driehoek in je vijftienhoek ingeschreven.