TOVEREN MET DRAAD EN KARTON

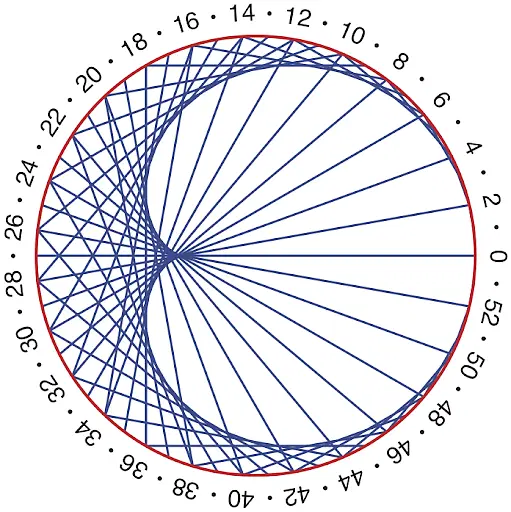
Als je in een een veelhoek van hoekpunt naar hoekpunt springt en de hoekpunten telkens met een draad verbindt, maak je kleinere veelhoeken binnenin de oorspronkelijke regelmatige veelhoek, als je tenminste altijd sprongetjes van dezelfde afstand maakt. Als de lengte van je sprongetjes (m) geen gemeenschappelijke deler heeft met het aantal hoekpunten van je veelhoek (n), dan is die kleinere veelhoek opnieuw een regelmatige veelhoek met n hoekpunten.. Als de lengte van je sprongetjes wel een gemeenschappelijke deler (d) heeft met het aantal hoekpunten van de veelhoek, dan krijg je een kleine veelhoek die niet n hoekpunten heeft, maar wel n/d hoekpunten. Bijvoorbeeld, bij een regelmatige vijftienhoek, de hoekpunten genummerd van 1 tot 15 in wijzerzin, kun je springen per 7 op volgende wijze: 1, 8, 15, 22=15+7=7, 14, 21=15+6=6, 13, 19=15+4=4, 11, 18=15+3=3, 10, 17=15+2=2, 9, 16=15+1=1 en zo ben je in vijftien stappen terug rond.

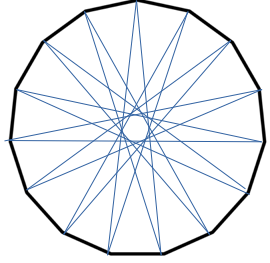
Kies je daarentegen voor sprongetjes per 5 dan heb je een gemeenschappelijke deler met 15 (5 namelijk). Dan spring je korter als volgt: 1, 6, 11, 16=15+1=1 en je bent rond en jet hebt een regelmatige driehoek in je vijftienhoek ingeschreven.

Waarom krijg je binnenin de regelmatige veelhoek terug een kleinere copie van de originele veelhoek? Dit komt door alle symmetrieen van de veelhoek.

Elke lijn die je van hoekpunt naar hoekpunt tekent, is parallel met een zijde van de oorspronkelijke veelhoek. Als je de lijnen altijd tekent met de zelfde sprong, dan zijn alle lijnen ook evenver verwijderd van hun oorspronkelijke parallelle zijde. Na alle sprongen van hoek naar hoek heb je dus evenveel lijnen die parallel zijn met en evenver liggen van de oorspronkelijke zijden van de veelhoek. Samen vormen ze een kleinere regelmatige veelhoek.

Als je de hoekpunten van de regelmatige veelhoeken onder elkaar met draad verbindt met sprongetjes van verschillende afstanden, dan kunnen er andere figuren ontstaan, meer bepaald als de verschillende afstanden een wiskundig verband onder elkaar hebben. Als je de hoekpunten met hun dubbel verbindt (1 met 2, 2 met 4, 3 met 6 enzoverder), dan zullen je lijnen langzamerhand een cardioide omschrijven, een hartvormige kromme binnenin de veelhoek.