verrassingen ontdekken in een driehoek

De driehoek van Pascal is eigenlijk een structuur van natuurlijke getallen die in een driehoeksvorm worden geordend. Je begint in de top met 1, daaronder 1 en 1, en op de volgende rij staan drie getallen, waarvan elk de som is van de twee getallen net erboven. Op de derde rij van je dus 1, 2 en 1, op de vierde rij 1, 3, 3, en 1 enzoverder.

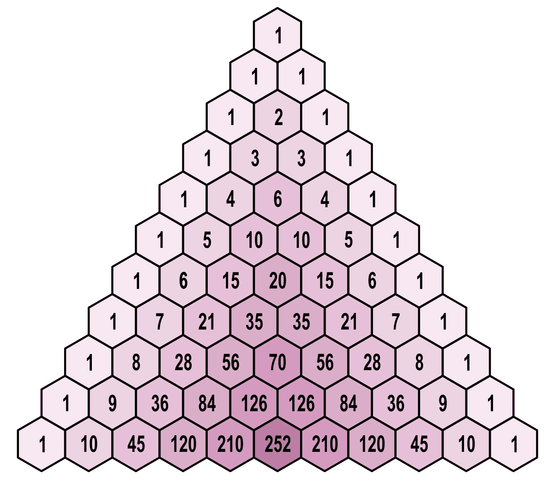
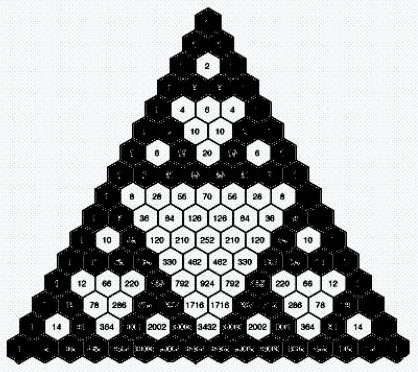
Deze driehoek was al bekend in het oude Indië, maar in de Europese traditie door Blaise Pascal in de 17de eeuw beschreven, en later naar hem vernoemd. De oorspronkelijke interesse in Pascals driehoek was vooral gemotiveerd door het berekenen van het aantal combinaties. Hierdoor komt het ook dat je de coëfficienten van het binomium (a+b)n terugvindt op de horizontale rijen. Bij n = 2 krijg je (a+b)² = aa + ab + ba + bb = 1.a² +2.ab+ 1.b². Bij n = 3 wordt het (a+b)³ = aaa+aab+aba+abb+baa+bab+bba+bbb = 1. a³+3. a²b+3.a b²+1. b³. Er zit nog meer in Pascals driehoek: bekijk in de figuur de evenwijdige rechten die getekend zijn door de driehoek en de som van de getallen van de vakjes waar je rechte doorgaat.

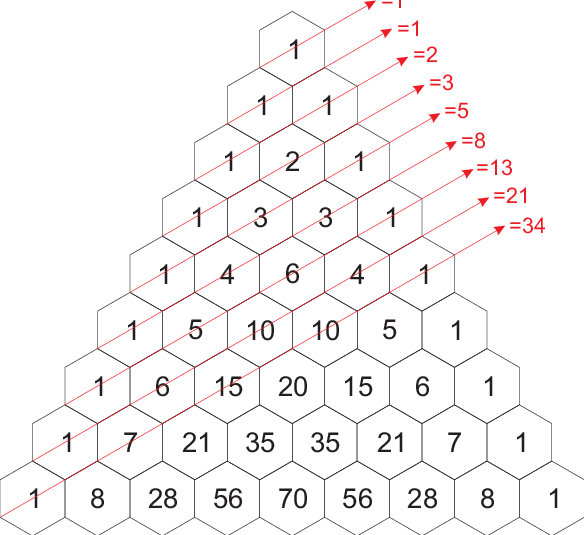
Dit is de rij van getallen van Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, enzovoort. Deze rij heeft ook wortels in de Oudheid maar is vernoemd naar de Italiaanse wiskundige Leonardo Pisano die in de late Middeleeuwen een encyclopedisch werk over de toenmalige wiskunde schreef. Tenslotte vind je in de driehoek van Pascal ook een connectie met fractalen Als je alle oneven getallen zwart kleurt, en de even getallen wit laat, dan duikt een patroon op in Pascals driehoek die bekend staat als de Sierpinski-driehoek, een driehoek waarin tot in der eeuwigheid kleinere driehoekjes opduiken. Fractalen zijn figuren die “zelfgelijkend” zijn, als je inzoomt op een fractale figuur, vind je dezelfde figuur terug. Als dus een stukje van de Sierpinski driehoek uitvergroot, zie je terug een Sierpinski-driehoek. Benoît Mandelbrot had in de jaren 1960 en 1970 heel wat patronen in zijn onderzoek ontdekt die deze eigenschap hadden en doopte ze uiteindelijk “fractalen”. In tegenstelling tot de klassieke figuren van de meetkunde hebben fractalen een “gebroken” (Hausdorff)dimensie. Terwijl een klassieke gewone driehoek dimensie 2 heeft, heeft de Sierpinski driehoek, door zijn “gaten”, dimensie 1,585 = log(3)/log(2).