EEN SCHAT ONTDEKKEN IN EEN KUBUS

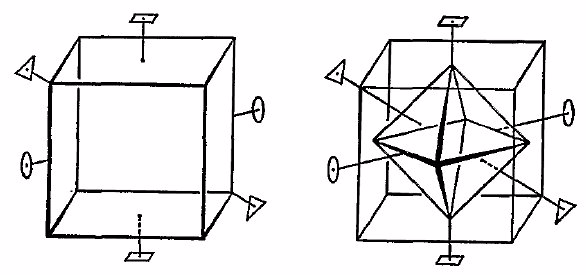
Men ziet in de figuur links een rood-blauw achtvlak (octaëder) in een groene kubus (hexaëder). In de tekeningen rechts: met elk zijvlak van de kubus komt een hoekpunt van de octaëder overeen en met elk hoekpunt van de kubus komt een zijvlak van de octaëder overeen. In de wiskunde: de octaëder is duaal aan de kubus en omgekeerd.

Als een ruimtelijk lichaam A een duaal is van een ander lichaam B, dan komt ieder zijvlak van A overeen met een hoekpunt van B, en ieder zijvlak van B met een hoekpunt van A.

• Een kubus en een octaëder zijn veelvlakken of polyeders. Het zijn ruimtelichamen die begrensd zijn door veelhoeken. Ze behoren beiden tot de meest regelmatige veelvlakken nl. tot de groep van de Platonische lichamen of veelvlakken begrensd door congruente regelmatige veelhoeken. Er zijn 5 Platonische lichamen.

Een kubus is het bekendste Platonische lichaam. Een kubus is begrensd door 6 congruente vierkanten.

Voor alle Platonische lichamen geldt de formule van Euler. In 1750 formuleerde Leonhard Euler de volgende stelling: H+Z-R=2 (H voor het aantal hoekpunten, Z voor het aantal zijvlakken en R voor het aantal ribben). Voor een kubus is H = 8, Z = 6 en R = 12 en 8 + 6 – 12 = 2. En voor een octaëder is H= 6, Z = 8 en R = 12 en 6 + 8 – 12 = 2.