EEN RUITKRISTAL MAKEN

Een ruitkristal of een rhombische dodecaëder is een ruimtelijk lichaam (3D-vorm) dat 12 gelijkzijdige ruiten als zijvlak heeft. De woorden “rhombische dodecaëder” komen via het Grieks in onze taal. Rhombisch betekent ruitvormig, dodecaëder staat voor twaalfvlak. Dus het is een ruitvormig twaalfvlak.

Een rhombische dodecaëder is een Catalan-lichaam, vernoemd naar de Belgische wiskundige Eugène Catalan (1814-1894). Een Catalan-lichaam is een duaal van een Archimedisch lichaam.

Dit vraagt om wat uitleg:

• Als je zegt dat een ruimtelijk lichaam A een duaal van een ander lichaam B is, wil je zeggen dat ieder zijvlak van A overeenkomt met een hoekpunt van B, en ieder zijvlak van B met een hoekpunt van A. In de nevenstaande figuur is de groene kubus een duaal van het rood-blauw achtvlak.

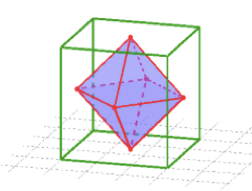
• Er zijn verschillende groepen ruimtelijke lichamen zoals bijvoorbeeld de veelvlakken of polyeders die begrensd zijn door veelhoeken. De meest regelmatige veelvlakken vormen de groep van de Platonische lichamen.

• Als een veelvlak begrensd is door congruente regelmatige veelhoeken spreekt men van een Platonisch lichaam. Een kubus is het bekendste Platonische lichaam. Een kubus is begrensd door 6 congruente vierkanten. Er zijn 5 Platonische lichamen.

• Een Archimedisch lichaam een ruimtelijk lichaam dat begrensd is door regelmatige veelhoeken en daarnaast ook symmetrisch is over zijn verticale en horizontale as. Deze lichamen, zijn vernoemd naar Archimedes, de grote Griekse wiskundige die ze als eerste beschreef. Er zijn slechts 13 verschillende Archimedische lichamen zoals je hier zier in de rechterkolom (de linkerkolom toont de Platonische lichamen die begrensd zijn door dezelfde soort veelhoek):

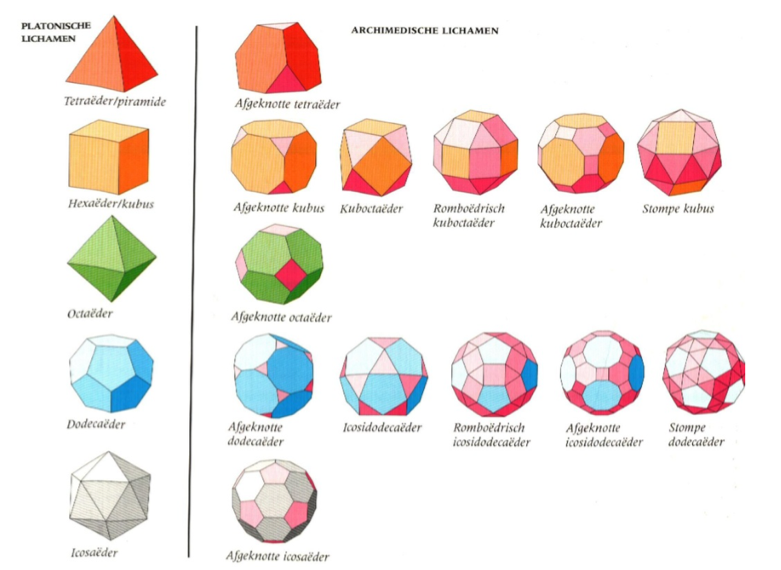
Bij deze Archimedische lichamen vind je de kuboctaëder (derde in de tweede rij hierboven). Dit lichaam is begrensd door vierkanten en gelijkzijdige driehoeken.

Het duale lichaam van deze kuboctaëder is nu de rhombische dodecaëder.

Net zoals bij alle lichamen die geen putten of stekels hebben (of die convex zijn, om de wiskundige technische term te gebruiken), geldt voor alle Platonische, Archimedische en Catalan-lichamen de formule van Euler. In 1750 formuleerde Leonhard Euler de volgende stelling: H+Z-R=2 (H voor het aantal hoekpunten, Z voor het aantal zijvlakken en R voor het aantal ribben). Voor een kubus is H = 8, Z = 6 en R = 12 en 8 + 6 – 12 = 2.

Hieruit volgt direct dat zowel voor de Archimedische kuboctaëder (met 12 hoekpunten en 14 zijvlakken) als rhombische dodecaëder (met 14 hoekpunten en 12 zijvlakken) je de volgende som hebt: 12+14-R=2, of het totaal aantal ribben van beide lichamen is 24.

1. Een convex lichaam is een lichaam waar elk lijnstuk waarmee je twee willekeurige punten van het lichaam verbindt, volledig binnen het lichaam ligt. In het geval van een ster met stekels bijvoorbeeld is het lijnstuk dat twee sterpunten verbindt niet binnenin de ster. Heb je een bal met een putje erin, dan is een lijnstuk dat twee punten van de put verbindt ook niet binnen de bal.